Prise d'un médicament

Un médicament est prescrit sous forme d’injections qui doivent être administrées une fois par semaine. Le volume de la première dose est déterminé en fonction de la masse corporelle du patient, à raison de \(2\) mL de médicament par kg.

Chaque semaine, le volume de la dose administrée est augmenté de \(5~\%\). Dès que le volume de la dose administrée est supérieur ou égal au double du volume initial, on réalise une dernière injection et on interrompt le traitement.

On applique le traitement à une personne dont la masse corporelle est de \(60\) kg.
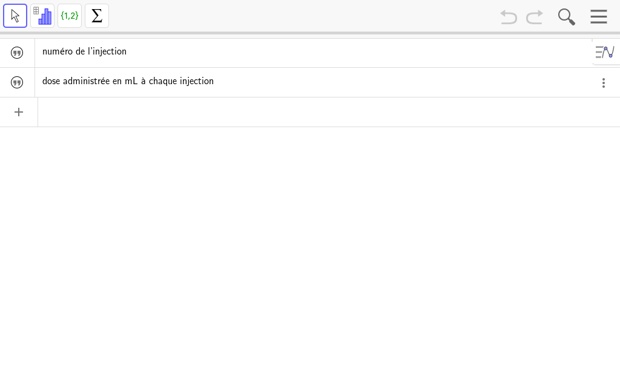
Pour déterminer les doses administrées, on s’aide de la feuille de calcul automatisé ci-dessous (les cellules de la plage [B2 : G2] sont paramétrées pour afficher les valeurs arrondies au dixième).

Tous les résultats seront arrondis au centième. 
1. Justifier que le nombre inscrit dans la case B2 est 120.
2. Calculer la dose administrée la deuxième semaine.
3. Donner la formule à saisir dans la cellule C2 qui, recopiée vers la droite, permet de calculer les valeurs des doses à administrer chaque semaine, puis la rentrer dans le tableur et afficher la dose à administrer chaque semaine.
4. On appelle \(V_n\) la valeur, en mL, du volume de la dose administrée lors de la \(n\)-ième injection. Ainsi, \(V_1 = 120\).
    a. Justifier que la suite \((V_n)\) est géométrique et préciser sa raison.
    b. Pour tout entier naturel \(n\), exprimer \(V_n\) en fonction de \(n\).
    c. Calculer le volume administré lors de la \(10^\text{e}\) injection.
5. a. Expliquer pourquoi le nombre total d’injections administrées lors du traitement peut s’obtenir en résolvant l’inéquation d’inconnue \(n\), entier naturel : \(120 \times 1{,}05^{n-1} \geqslant 240\).
    b. Justifier que le traitement comporte au total \(16\) injections.
    c. Déterminer le volume total de médicament administré au patient lors de l’ensemble du traitement. Arrondir au centième de mL.

D'après Bac session 2019 , métropole, série ST2S.